domingo, 4 de noviembre de 2012
sábado, 25 de agosto de 2012
miércoles, 25 de julio de 2012
sábado, 9 de junio de 2012
6.1.1 Definición de Limites:
La idea de límite es central en el estudio del cálculo y ha sido usada en muy diversas formas a través de los siglos. Desde los Griegos varios siglos antes de Cristo, en el método de exhausión, donde Arquímedes ocupa un lugar muy importante, varios siglos más tarde Newton la usó en sus famosos fluxiones con los cuales desarrolló el cálculo y Cauchy que formalizó la idea con la definición que conocemos en nuestros días.
6.1.2 Historia de los Limites:
Los antiguos griegos utilizaban procedimientos basados en límites para calcular áreas, como el área del círculo , utilizando el <<>>.consistía en cubrir o ( agotar) una región de forma tan completa como fuera posible utilizando triángulos. sumando las áreas de los triángulos se tenía una aproximación al área de la región de interés. Newton y Leibniz, los inventores del cálculo . sin embargo. no dieron una definición rigurosa del procedimiento.El matemático francés Augustine-louis cauchy(1789-1857) fue el primero en desarrollar una definición rigurosa de límite. la definición que usaremos aquí se remonta al matemático alemán Karl Weierstrass (1815-1897)
6.1.3 Cuales matemáticos fueron los primeros que hablaron sobre los Limites:
Gottfried Wilhelm Leibniz:
La invención del cálculo infinitesimal es
atribuida tanto a Leibniz como a Newton. De acuerdo con los
cuadernos de Leibniz, el 11 de noviembre de 1675 tuvo lugar un acontecimiento
fundamental, ese día empleó por primera vez el cálculo integral para encontrar
el área bajo la curva de una función y=f(x).
Sir Isaac Newton:
De 1667 a 1669 emprendió
investigaciones sobre óptica y fue elegido fellow del Trinity
College. En 1669 su mentor, Isaac
Barrow, renunció a su Cátedra
Lucasiana de matemática, puesto
en el que Newton le sucedería hasta 1696. El mismo año envió a John Collins, por medio de Barrow, su "Analysis per aequationes
número terminorum infinitos". Para Newton, este manuscrito representa
la introducción a un potente método general, que desarrollaría más tarde: su cálculo
diferencial e integral.
jueves, 12 de abril de 2012
jueves, 29 de marzo de 2012
1.1 Historia de la Geometría
Geometría (del griego geo, 'tierra'; metrein, 'medir'), rama de las matemáticas que se ocupa de las propiedades del espacio. En su forma más elemental, la geometría se preocupa de problemas métricos como el cálculo del área y diámetro de figuras planas y de la superficie y volumen de cuerpos sólidos. Otros campos de la geometría son la geometría analítica, geometría descriptiva, topología, geometría de espacios con cuatro o más dimensiones, geometría fractal, y geometría no euclídea.
1.2 Grandes Físico, Filósofos y Matemáticos
Niels Henrik Abel (1802 – 1829)
Matemático noruego. Interesado desde muy joven (1817) por la teoría de las ecuaciones algebraicas , creyó, en un principio, haber encontrado una fórmula para la resolución por radicales de la ecuación general de 5º grado, pero en 1824 demostró la irresolubilidad por este método para grados superiores al cuarto. Cargó con los gastos de publicar el trabajo y apoyado por sus profesores.
María Gaetana Agnesi(1718 - 1799) María G. Agnesi nació en Milán en 1718, y murió también en Milán en 1799, fue una distinguida lingüista , matemática y filósofa; remplazó a su padre en la cátedra de matemáticas de la Universidad de Bologna cuando éste estuvo enfermo, y fue la primera mujer en ocupar una cátedra de matemáticas. En 1748, se publicó su libro "Instituzioni Analithe" sobre cálculo diferencial, que fue muy popular; se tradujo a muchos idiomas y se usó en Europa durante muchos años.
René Descartes ( 1596 – 1650 ) René Descartes nació en Turena, Francia, en 1596, de familia bien acomodada. Fue un muchacho inteligente, que, a los 8 años, envió su padre al colegio de La Flèche , recién abierto por los jesuitas. Era, como Descartes afirmó más tarde, una de las Escuelas más famosas de Europa.
Euclides (s. III a.c.) Matemático griego. Vivió en Alejandría y el único hecho seguro que se conoce de su vida es que hacia el año -300 era profesor de geometría en esta ciudad. Su obra principal es los Elementos, compuesta de 13 libros y dos más que no se atribuyen a él; en ella establece las definiciones, axiomas y postulados indemostrables, a partir de los cuales van sucediéndose los teoremas en un orden estrictamente lógico.
Isaac Newton, (1642-1727) Físico y matemático inglés. Entró en 1661 como estudiante en el Trinity College, de Cambridge. En 1669 fue nombrado profesor en sustitución de su maestro Barrow. Ejerció su magisterio en Cambridge hasta 1696. A partir de entonces vivió en Londres, donde fue nombrado sucesivamente inspector de la Moneda (1696), director de la Moneda (1699) y presidente de la Royal Society, cargo este último para el cual fue reelegido (1703) año tras año hasta su muerte.
Sus contribuciones más decisivas en el campo de la física están expuestas en los Philosophiae naturalis principia mathematica (1687). En esta obra se introducen los conceptos fundamentales de la mecánica, a la vez que se exponen los axiomas a que satisfacen. También en esta obra enunció la ley de la atracción universal, que generaliza y da forma matemática, en una síntesis magistral, a la identidad causal entre fenómenos tales como la caída de los cuerpos, las mareas y el movimiento de los planetas alrededor del Sol.
Pitágoras ( 570 a.c. - 496 a.c.) Filósofo y matemático griego. Nació en Samos. Aunque no se poseen datos ciertos de su vida, parece que estuvo en contacto con sacerdotes egipcios que agudizaron su interés por la especulación matemática. Su auténtico interés radica en ser el fundador de una secta místico-religiosa caracterizada por su dedicación al estudio de las matemáticas y por practicar un tipo de vida comunitaria de fuertes resonancias órficas. La aportación filosófica de Pitágoras es inseparable del conjunto doctrinal que llamamos pitagorismo. Se le atribuye la invención de la tabla de multiplicar, del sistema decimal, de las proporciones aritméticas y del teorema que lleva su nombre.
1.3 Definición de Geometría
La geometría es una parte de la matemática que trata de estudiar unas idealizaciones del espacio en que vivimos, que son los puntos, las rectas y los planos, y otros elementos conceptuales derivados de ellos, como polígonos o poliedros.
En la practica, la geometría sirve para solucionar problemas concretos en el mundo de lo visible. Entre sus utilidades se encuentran la justificación teórica de muchos instrumentos: compás, teodolito, pantógrafo, sistema de posicionamiento global. También es la que nos permite medir areas y volumenes, es útil en la preparación de diseños, e incluso en la fabricación de artesanías.
2.1 Punto, Recta, Semirrecta y Segmento
Punto: En geometría el punto es uno de los entes geométricos fundamentales, junto a la recta y el plano. Son considerados conceptos primarios, o sea que no es posible definirlos con el uso de otros elementos ya conocidos.
 Recta: En geometría euclidiana, la recta o linea recta, se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos punto y esta compuesta de infinitos segmentos. También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, o sea, no posee principio ni fin.
Recta: En geometría euclidiana, la recta o linea recta, se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos punto y esta compuesta de infinitos segmentos. También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, o sea, no posee principio ni fin.
 Semirrecta: La semirrecta, por lo tanto, es la parte de una recta que está formada por todos los puntos que se ubican hacia un lado de un punto fijo: esto quiere decir que una semirrecta tiene un primer punto (el origen) pero se extiende hacia el infinito. La recta, en cambio, no tiene ni principio ni fin.
Semirrecta: La semirrecta, por lo tanto, es la parte de una recta que está formada por todos los puntos que se ubican hacia un lado de un punto fijo: esto quiere decir que una semirrecta tiene un primer punto (el origen) pero se extiende hacia el infinito. La recta, en cambio, no tiene ni principio ni fin.
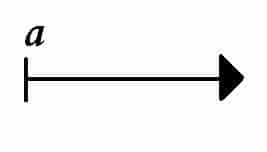 Segmento: Segmento es la porción de recta limitada por dos puntos, llamados extremos.
Segmento: Segmento es la porción de recta limitada por dos puntos, llamados extremos.




2.2 Ángulos y Clases de Ángulos
Un angulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. Suelen medirse en unidades tales como el radian, el grado sexagesimal o el grado centesimal.
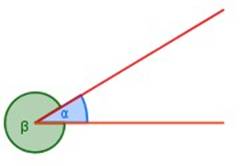
CLASES DE ANGULO:
Al ángulo α se le llama ángulo convexo, mientras que el ángulo β es cóncavo.
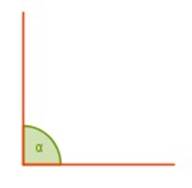
 Ángulo recto: es aquel cuya medida es de 90°
Ángulo recto: es aquel cuya medida es de 90°
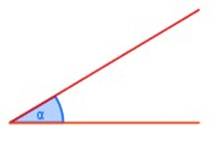
 Ángulo agudo: es aquel cuya medida es menor que 90°
Ángulo agudo: es aquel cuya medida es menor que 90°
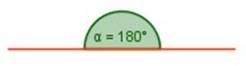
 Ángulo extendido: es aquel cuya medida es de 180°
Ángulo extendido: es aquel cuya medida es de 180°
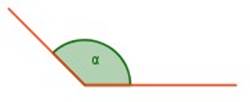
 Ángulo obtuso: es aquel cuya medida es mayor que 90° y menor que 180°
Ángulo obtuso: es aquel cuya medida es mayor que 90° y menor que 180°
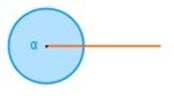
 Ángulo completo: es aquel cuya medida es de 360°
Ángulo completo: es aquel cuya medida es de 360°
CLASES DE ANGULO:
Al ángulo α se le llama ángulo convexo, mientras que el ángulo β es cóncavo.






2.3 Mediatriz y Bisectriz
Mediatriz: La mediatriz de un segmento es la recta perpendicular a dicho segmento trazado por su punto medio. Equivalentemente se puede definir como la recta cuyos puntos son equidistantes a los extremos del segmento. Tambien se la llama simetral.
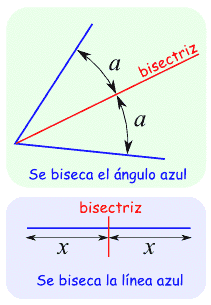
Bisectriz: La línea que divide algo en dos partes iguales.Puedes bisectar líneas, ángulos, y otras cosas.

2.4 Recta Paralela y Recta Perpendicular
Recta Paralela: Dos rectas que no se cruzan en ningún punto del plano
 Recta Perpendicular: Dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos iguales.
Recta Perpendicular: Dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos iguales.



3.1 Definición de Polígonos
Polígono: En geometría, un poligono es una figura plana que esta limitada por una curva cerrada, compuesta por una secuencia finita de segmentos rectos. Estos segmentos son llamados lados, y los puntos en que se intersectan se llaman vértices.


3.2 Tipos de Polígonos
Polígono cruzado: Dos o mas lados se cortan. Los polígonos regulares estrellados son el caso más interesante





Polígono convexo: Si el segmento que une dos puntos cualesquiera del polígono es interior al polígono. Todos los ángulos interiores son menores de 180º. Si uno o más de los ángulos interiores es mayor de 180, el polígono es no convexo, o cóncavo.

Polígono regular: Si tiene lados y ángulos iguales. El representado a la derecha es polígono equilátero,(lados iguales) pero no es regular (ángulos no iguales)

Polígono estrellado: Son los polígonos que se construyen a partir de trazar diagonales en polígonos regulares. Se obtienen diferentes construcciones dependiendo de la unión de los vértices: de dos en dos, de tres en tres, etc.

4.1 Definición de Triángulo
Un triangulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vertices y los segmentos de recta determinados son los lados del triangulo. Dos lados contiguos forman uno de los ángulos interiores del triangulo.

4.2 Teoremas de Pitágoras
Un ángulo recto se puede definir como el ángulo formado cuando dos líneas rectas se cruzan de tal forma que los cuatro ángulos que forman son iguales. El teorema también se puede definir de otra forma: si las longitudes de los tres lados (a,b,c) de un triángulo satisfacen la relación anterior, el ángulo entre los lados a y b debe ser de 90 grados.
Por ejemplo, un triángulo con los lados a = 3, b = 4, c = 5 (pulgadas, pies, metros,... lo que sea) es rectángulo porque
a2 + b2 = 32 + 42
= 9 + 16 = 25 = c2
a2 + b2 = c2
Por ejemplo, un triángulo con los lados a = 3, b = 4, c = 5 (pulgadas, pies, metros,... lo que sea) es rectángulo porque
= 9 + 16 = 25 = c2
Si un triángulo tiene lados de longitud (a,b,c), con los lados (a,b) formando un ángulo de 90 grados ("ángulo recto"), tenemos que
4.3 Triángulo Equilátero
Triangulo Equilatero: Un triángulo equilátero, es un polígono de tres lados iguales y tres ángulos agudos e iguales a 60°, este triángulo es simétrico respecto a sus tres alturas. La altura de un triángulo equilatero es igual a.
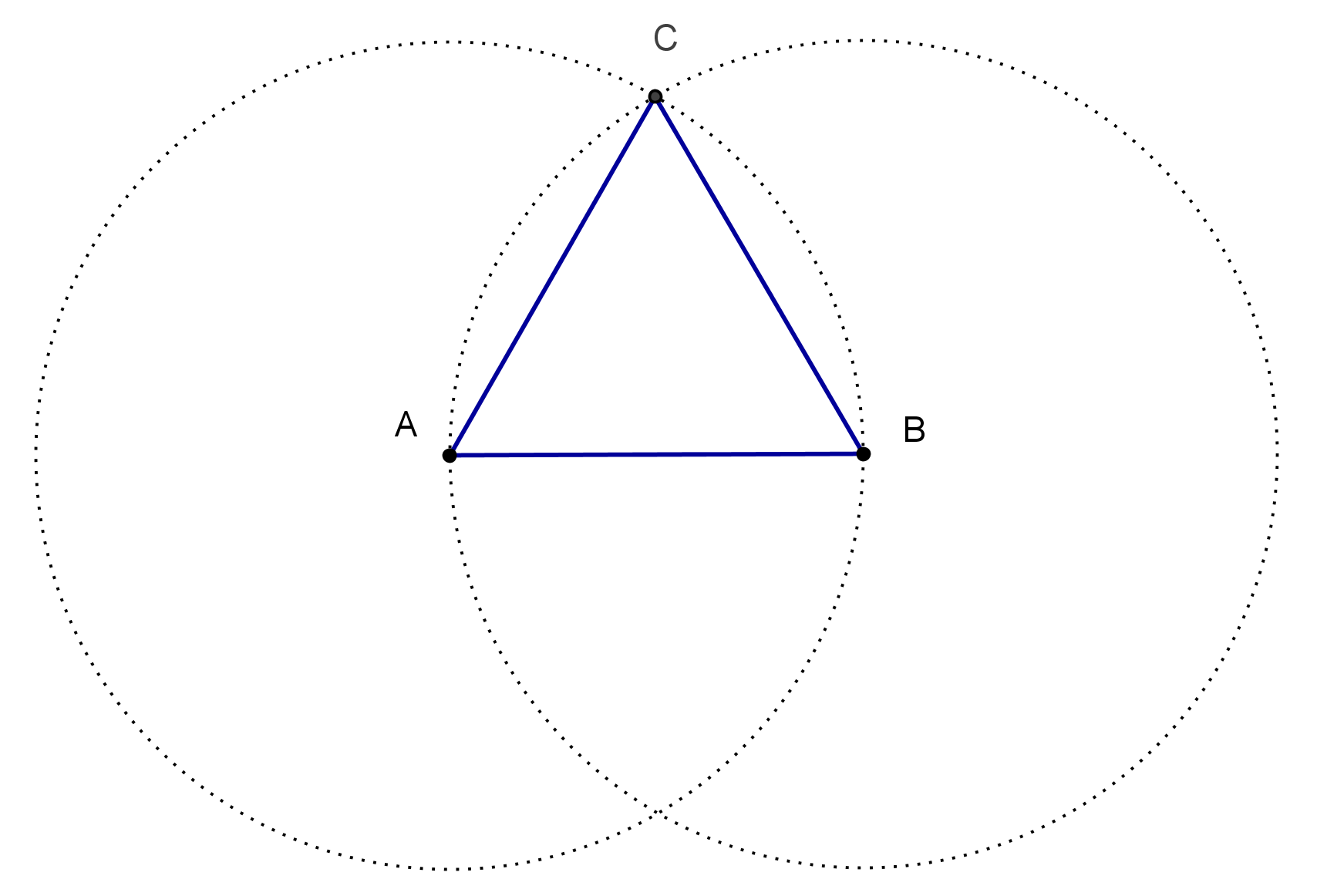

4.4 Triángulo Isósceles
Triangulo Isósceles: Es el que tiene dos lados de igual medida, por lo tanto, tiene dos ángulos de igual medida.
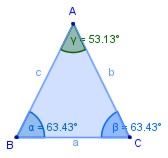
trazo AB = trazo AC
∠ ABC = ∠ BCA

Suscribirse a:
Entradas (Atom)







